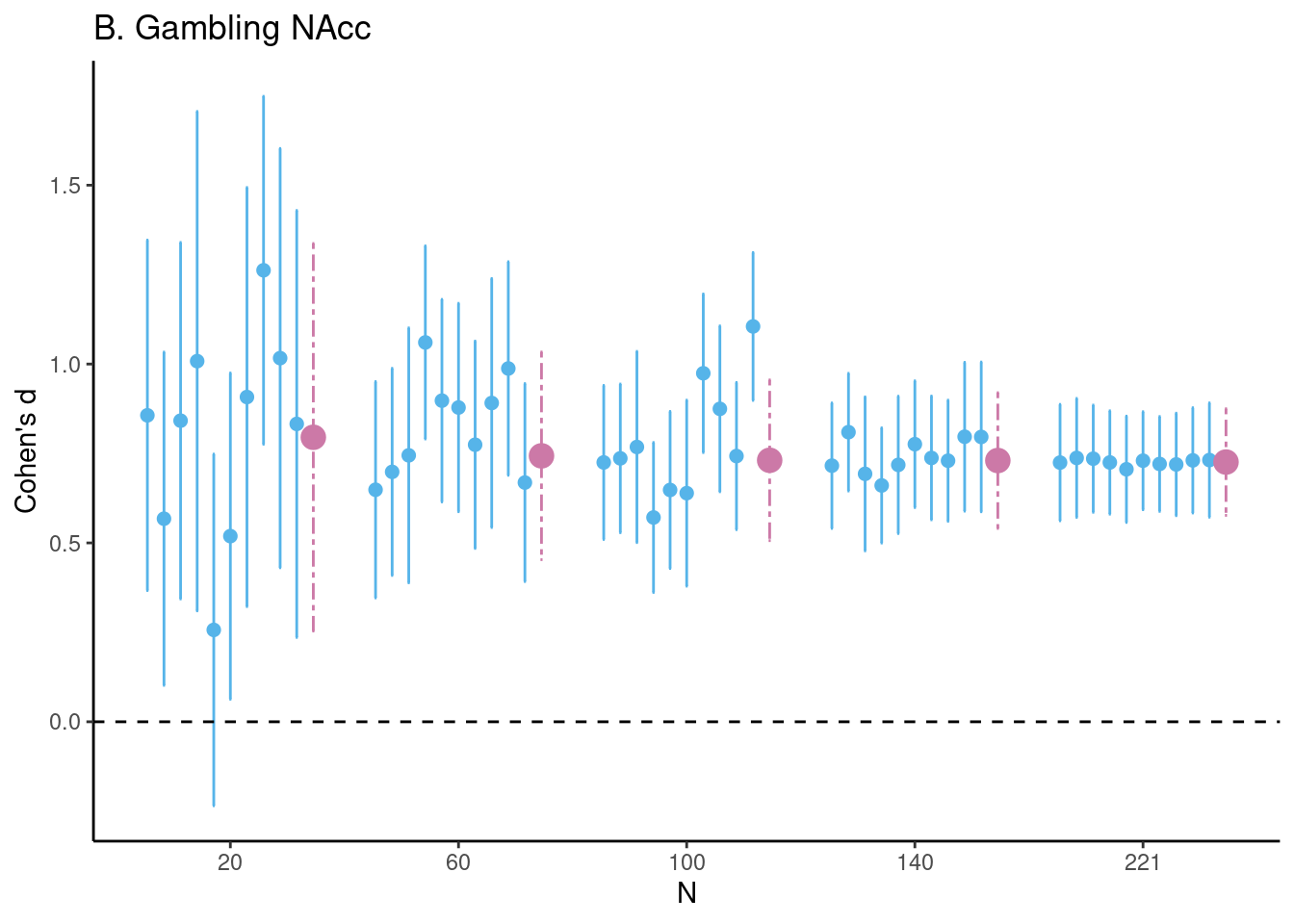
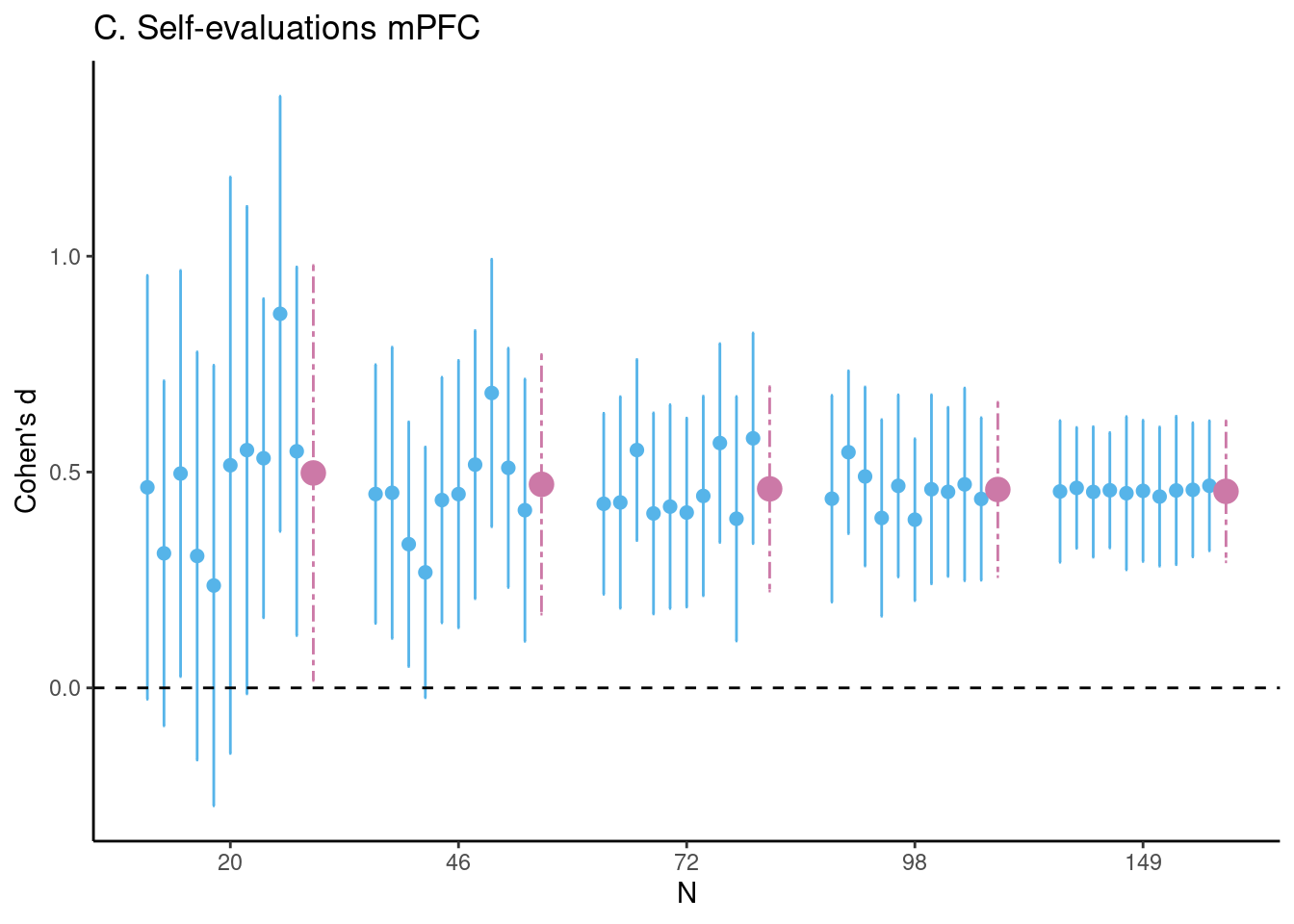
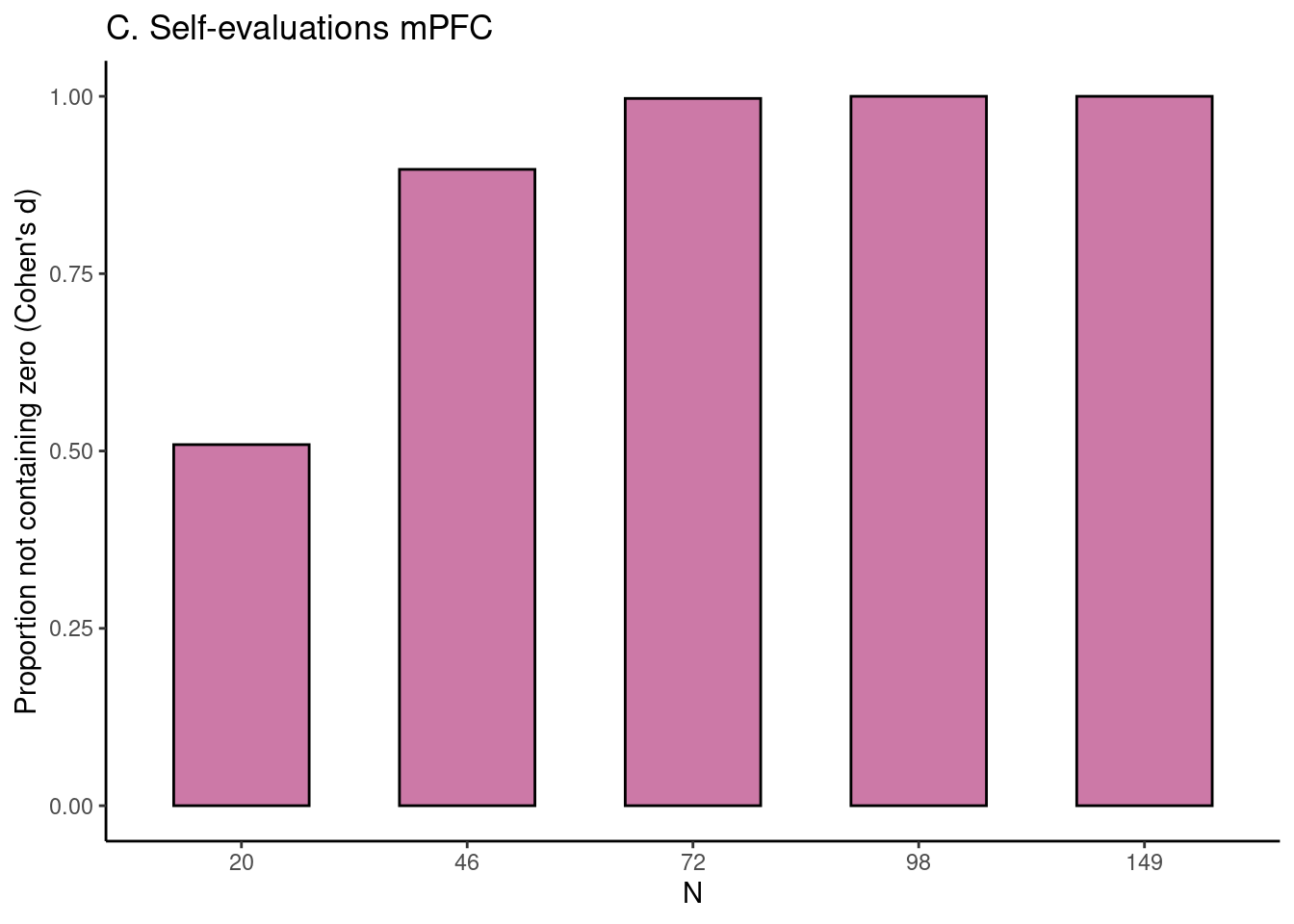
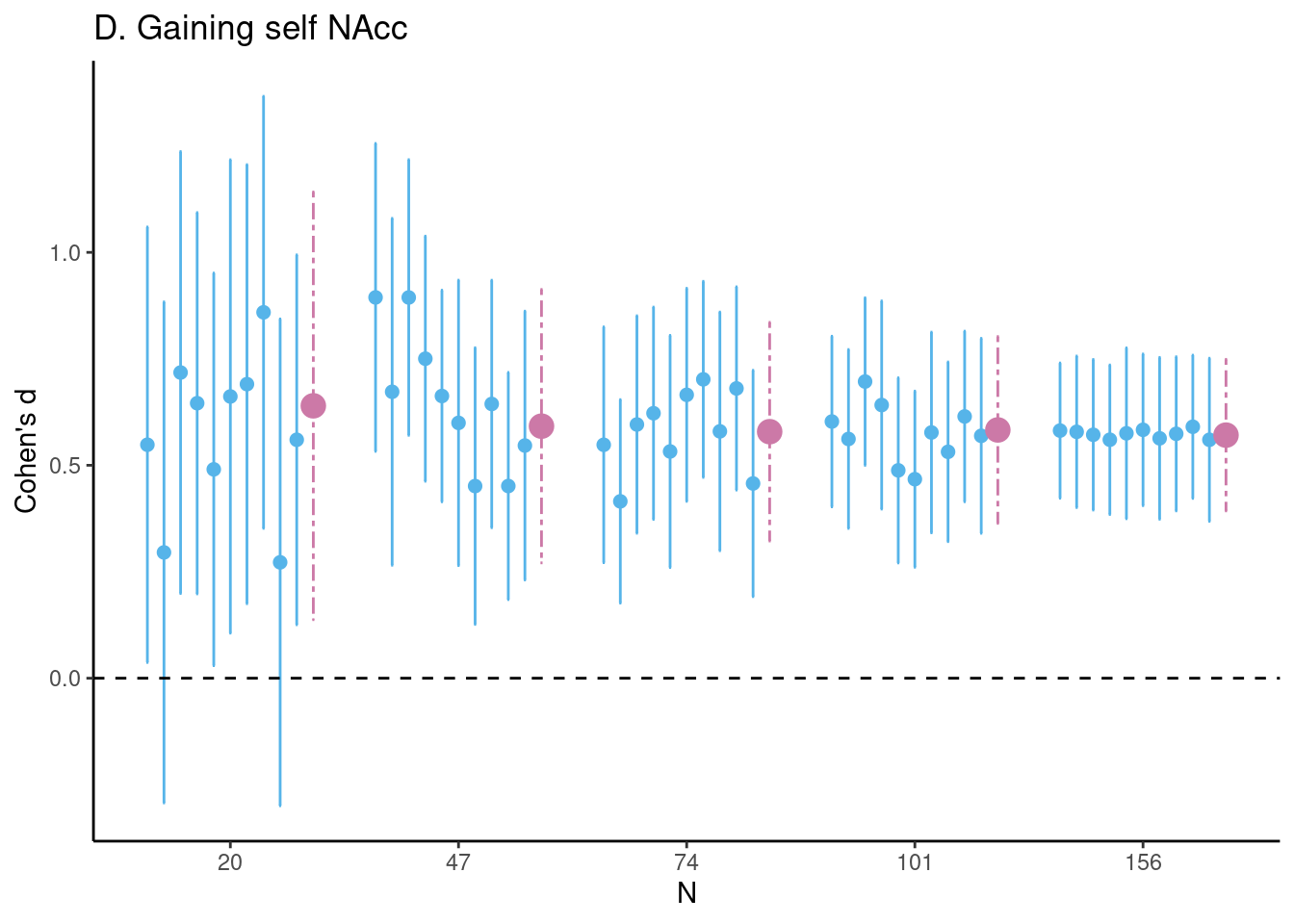
Achterberg, Michelle, and Mara van der Meulen. 2019.
“Genetic and Environmental Influences on MRI Scan Quantity and Quality.” Developmental Cognitive Neuroscience 38 (August): 100667.
https://doi.org/10.1016/j.dcn.2019.100667.
Baker, Daniel H., Greta Vilidaite, Freya A. Lygo, Anika K. Smith, Tessa R. Flack, André D. Gouws, and Timothy J. Andrews. 2021.
“Power Contours: Optimising Sample Size and Precision in Experimental Psychology and Human Neuroscience.” Psychological Methods 26 (3): 295–314.
https://doi.org/10.1037/met0000337.
Bennett, Craig M., and Michael B. Miller. 2013.
“fMRI Reliability: Influences of Task and Experimental Design.” Cognitive, Affective, & Behavioral Neuroscience 13 (4): 690–702.
https://doi.org/10.3758/s13415-013-0195-1.
Bishop, Dorothy. 2019.
“Rein in the Four Horsemen of Irreproducibility.” Nature 568 (7753): 435–35.
https://doi.org/10.1038/d41586-019-01307-2.
Braams, Barbara R., Sabine Peters, Jiska S. Peper, Berna Güroğlu, and Eveline A. Crone. 2014.
“Gambling for Self, Friends, and Antagonists: Differential Contributions of Affective and Social Brain Regions on Adolescent Reward Processing.” NeuroImage 100 (October): 281–89.
https://doi.org/10.1016/j.neuroimage.2014.06.020.
Brett, Matthew, Jean-Luc Anton, Romain Valabregue, and Jean-Baptiste Poline. 2002. “Region of Interest Analysis Using an SPM Toolbox.” 8th International Conference on Functional Mapping of the Human Brain 16 (2): 497.
Button, Katherine S., John P. A. Ioannidis, Claire Mokrysz, Brian A. Nosek, Jonathan Flint, Emma S. J. Robinson, and Marcus R. Munafò. 2013.
“Power Failure: Why Small Sample Size Undermines the Reliability of Neuroscience.” Nature Reviews Neuroscience 14 (5): 365–76.
https://doi.org/10.1038/nrn3475.
Calabro, Finnegan J, David F Montez, Bart Larsen, Charles M Laymon, William Foran, Michael N Hallquist, Julie C Price, and Beatriz Luna. 2023.
“Striatal Dopamine Supports Reward Expectation and Learning: A Simultaneous PET/fMRI Study.” NeuroImage 267 (February): 119831.
https://doi.org/10.1016/j.neuroimage.2022.119831.
Casey, B. J., Tariq Cannonier, May I. Conley, Alexandra O. Cohen, Deanna M. Barch, Mary M. Heitzeg, Mary E. Soules, et al. 2018.
“The Adolescent Brain Cognitive Development (ABCD) Study: Imaging Acquisition Across 21 Sites.” Developmental Cognitive Neuroscience, The adolescent brain cognitive development (ABCD) consortium: Rationale, aims, and assessment strategy, 32 (August): 43–54.
https://doi.org/10.1016/j.dcn.2018.03.001.
Chen, Gang, Daniel S. Pine, Melissa A. Brotman, Ashley R. Smith, Robert W. Cox, Paul A. Taylor, and Simone P. Haller. 2022.
“Hyperbolic Trade-Off: The Importance of Balancing Trial and Subject Sample Sizes in Neuroimaging.” NeuroImage 247 (February): 118786.
https://doi.org/10.1016/j.neuroimage.2021.118786.
Cohen, Jacob. 1992.
“A Power Primer.” Psychological Bulletin 112 (1): 155–59.
https://doi.org/10.1037/0033-2909.112.1.155.
Crone, Eveline A., Anna C. K. van Duijvenvoorde, and Jiska S. Peper. 2016.
“Annual Research Review: Neural Contributions to Risk-Taking in Adolescence Developmental Changes and Individual Differences.” Journal of Child Psychology and Psychiatry 57 (3): 353–68.
https://doi.org/10.1111/jcpp.12502.
Crone, Eveline A., Kayla H. Green, Ilse H. van de Groep, and Renske van der Cruijsen. 2022.
“A Neurocognitive Model of Self-Concept Development in Adolescence.” Annual Review of Developmental Psychology 4 (Volume 4, 2022): 273–95.
https://doi.org/10.1146/annurev-devpsych-120920-023842.
Crone, Eveline A., and Nikolaus Steinbeis. 2017.
“Neural Perspectives on Cognitive Control Development during Childhood and Adolescence.” Trends in Cognitive Sciences 21 (3): 205–15.
https://doi.org/10.1016/j.tics.2017.01.003.
Cruijsen, Renske van der, Neeltje E Blankenstein, Jochem P Spaans, Sabine Peters, and Eveline A Crone. 2023.
“Longitudinal Self-Concept Development in Adolescence.” Social Cognitive and Affective Neuroscience 18 (1): nsac062.
https://doi.org/10.1093/scan/nsac062.
Denny, Bryan T., Hedy Kober, Tor D. Wager, and Kevin N. Ochsner. 2012.
“A Meta-Analysis of Functional Neuroimaging Studies of Self- and Other Judgments Reveals a Spatial Gradient for Mentalizing in Medial Prefrontal Cortex.” Journal of Cognitive Neuroscience 24 (8): 1742–52.
https://doi.org/10.1162/jocn_a_00233.
Dick, Anthony Steven, Daniel A. Lopez, Ashley L. Watts, Steven Heeringa, Chase Reuter, Hauke Bartsch, Chun Chieh Fan, et al. 2021.
“Meaningful Associations in the Adolescent Brain Cognitive Development Study.” NeuroImage 239 (October): 118262.
https://doi.org/10.1016/j.neuroimage.2021.118262.
Efron, Bradley, and R. J. Tibshirani. 1994.
An Introduction to the Bootstrap. New York: Chapman; Hall/CRC.
https://doi.org/10.1201/9780429246593.
Elliott, Maxwell L., Annchen R. Knodt, David Ireland, Meriwether L. Morris, Richie Poulton, Sandhya Ramrakha, Maria L. Sison, Terrie E. Moffitt, Avshalom Caspi, and Ahmad R. Hariri. 2020.
“What Is the Test-Retest Reliability of Common Task-Functional MRI Measures? New Empirical Evidence and a Meta-Analysis.” Psychological Science 31 (7): 792–806.
https://doi.org/10.1177/0956797620916786.
Funder, David C., and Daniel J. Ozer. 2019.
“Evaluating Effect Size in Psychological Research: Sense and Nonsense.” Advances in Methods and Practices in Psychological Science 2 (2): 156–68.
https://doi.org/10.1177/2515245919847202.
Gelman, Andrew, and John Carlin. 2014.
“Beyond Power Calculations: Assessing Type S (Sign) and Type M (Magnitude) Errors.” Perspectives on Psychological Science 9 (6): 641–51.
https://doi.org/10.1177/1745691614551642.
Gignac, Gilles E., and Eva T. Szodorai. 2016.
“Effect Size Guidelines for Individual Differences Researchers.” Personality and Individual Differences 102 (November): 74–78.
https://doi.org/10.1016/j.paid.2016.06.069.
Herting, Megan M., Cory Johnson, Kathryn L. Mills, Nandita Vijayakumar, Meg Dennison, Chang Liu, Anne-Lise Goddings, et al. 2018.
“Development of Subcortical Volumes Across Adolescence in Males and Females: A Multisample Study of Longitudinal Changes.” NeuroImage 172 (May): 194–205.
https://doi.org/10.1016/j.neuroimage.2018.01.020.
Ioannidis, John P. A. 2005.
“Why Most Published Research Findings Are False.” PLOS Medicine 2 (8): e124.
https://doi.org/10.1371/journal.pmed.0020124.
Klapwijk, Eduard T., Wouter van den Bos, Christian K. Tamnes, Nora M. Raschle, and Kathryn L. Mills. 2021.
“Opportunities for Increased Reproducibility and Replicability of Developmental Neuroimaging.” Developmental Cognitive Neuroscience 47 (February): 100902.
https://doi.org/10.1016/j.dcn.2020.100902.
Klapwijk, Eduard, Herbert Hoijtink, and Joran Jongerling. 2024.
neuroUp: Plan Sample Size for fMRI Regions of Interest Research Using Bayesian Updating. Zenodo.
https://doi.org/10.5281/zenodo.11526169.
Marek, Scott, Brenden Tervo-Clemmens, Finnegan J. Calabro, David F. Montez, Benjamin P. Kay, Alexander S. Hatoum, Meghan Rose Donohue, et al. 2022.
“Reproducible Brain-Wide Association Studies Require Thousands of Individuals.” Nature 603 (7902): 654–60.
https://doi.org/10.1038/s41586-022-04492-9.
Maxwell, Scott E. 2004.
“The Persistence of Underpowered Studies in Psychological Research: Causes, Consequences, and Remedies.” Psychological Methods 9 (2): 147–63.
https://doi.org/10.1037/1082-989X.9.2.147.
Munafò, Marcus R., Brian A. Nosek, Dorothy V. M. Bishop, Katherine S. Button, Christopher D. Chambers, Nathalie Percie du Sert, Uri Simonsohn, Eric-Jan Wagenmakers, Jennifer J. Ware, and John P. A. Ioannidis. 2017.
“A Manifesto for Reproducible Science.” Nature Human Behaviour 1 (1): 0021.
https://doi.org/10.1038/s41562-016-0021.
Nord, Camilla L., Vincent Valton, John Wood, and Jonathan P. Roiser. 2017.
“Power-up: A Reanalysis of ’Power Failure’ in Neuroscience Using Mixture Modeling.” Journal of Neuroscience 37 (34): 8051–61.
https://doi.org/10.1523/JNEUROSCI.3592-16.2017.
Nüst, Daniel, and Stephen J. Eglen. 2021.
“CODECHECK: An Open Science Initiative for the Independent Execution of Computations Underlying Research Articles During Peer Review to Improve Reproducibility.” https://doi.org/10.12688/f1000research.51738.2.
Open Science Collaboration. 2015.
“Estimating the Reproducibility of Psychological Science.” Science 349 (6251): aac4716.
https://doi.org/10.1126/science.aac4716.
Peters, Sabine, Barbara R. Braams, Maartje E. J. Raijmakers, P. Cédric M. P. Koolschijn, and Eveline A. Crone. 2014.
“The Neural Coding of Feedback Learning Across Child and Adolescent Development.” Journal of Cognitive Neuroscience 26 (8): 1705–20.
https://doi.org/10.1162/jocn_a_00594.
Peters, Sabine, and Eveline A. Crone. 2017.
“Increased Striatal Activity in Adolescence Benefits Learning.” Nature Communications 8 (1): 1983.
https://doi.org/10.1038/s41467-017-02174-z.
Poldrack, R. A., C. I. Baker, J. Durnez, K. J. Gorgolewski, P. M. Matthews, M. R. Munafo, T. E. Nichols, J. B. Poline, E. Vul, and T. Yarkoni. 2017.
“Scanning the Horizon: Towards Transparent and Reproducible Neuroimaging Research.” Nature Reviews Neuroscience 18 (2): 115–26.
https://doi.org/10.1038/nrn.2016.167.
R Core Team. 2023.
R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing.
https://www.R-project.org/.
Röseler, Lukas. 2024.
“CODECHECK Certificate 2024-005,” October.
https://doi.org/10.5281/ZENODO.13945051.
Rouder, Jeffrey N. 2014.
“Optional Stopping: No Problem for Bayesians.” Psychonomic Bulletin & Review 21 (2): 301–8.
https://doi.org/10.3758/s13423-014-0595-4.
Satterthwaite, Theodore D., John J. Connolly, Kosha Ruparel, Monica E. Calkins, Chad Jackson, Mark A. Elliott, David R. Roalf, et al. 2016.
“The Philadelphia Neurodevelopmental Cohort: A Publicly Available Resource for the Study of Normal and Abnormal Brain Development in Youth.” NeuroImage, Sharing the wealth: Brain Imaging Repositories in 2015, 124 (January): 1115–19.
https://doi.org/10.1016/j.neuroimage.2015.03.056.
Schönbrodt, Felix D., and Marco Perugini. 2013.
“At What Sample Size Do Correlations Stabilize?” Journal of Research in Personality 47 (5): 609–12.
https://doi.org/10.1016/j.jrp.2013.05.009.
Schreuders, Elisabeth, Barbara R. Braams, Neeltje E. Blankenstein, Jiska S. Peper, Berna Güroğlu, and Eveline A. Crone. 2018.
“Contributions of Reward Sensitivity to Ventral Striatum Activity Across Adolescence and Early Adulthood.” Child Development 89 (3): 797–810.
https://doi.org/10.1111/cdev.13056.
Schumann, G., E. Loth, T. Banaschewski, A. Barbot, G. Barker, C. Büchel, P. J. Conrod, et al. 2010.
“The IMAGEN Study: Reinforcement-Related Behaviour in Normal Brain Function and Psychopathology.” Molecular Psychiatry 15 (12): 1128–39.
https://doi.org/10.1038/mp.2010.4.
Somerville, Leah H., Susan Y. Bookheimer, Randy L. Buckner, Gregory C. Burgess, Sandra W. Curtiss, Mirella Dapretto, Jennifer Stine Elam, et al. 2018.
“The Lifespan Human Connectome Project in Development: A Large-Scale Study of Brain Connectivity Development in 521 Year Olds.” NeuroImage 183 (December): 456–68.
https://doi.org/10.1016/j.neuroimage.2018.08.050.
Spaans, Jochem, Sabine Peters, Andrik Becht, Renske van der Cruijsen, Suzanne van de Groep, and Eveline A. Crone. 2023.
“Longitudinal Neural and Behavioral Trajectories of Charity Contributions Across Adolescence.” Journal of Research on Adolescence 33 (2): 480–95.
https://doi.org/10.1111/jora.12820.
Szucs, Denes, and John P. A. Ioannidis. 2017.
“Empirical Assessment of Published Effect Sizes and Power in the Recent Cognitive Neuroscience and Psychology Literature.” PLOS Biology 15 (3): e2000797.
https://doi.org/10.1371/journal.pbio.2000797.
Turner, Benjamin O., Erick J. Paul, Michael B. Miller, and Aron K. Barbey. 2018.
“Small Sample Sizes Reduce the Replicability of Task-Based fMRI Studies.” Communications Biology 1 (1).
https://doi.org/10.1038/s42003-018-0073-z.
Wicherts, Jelte M., Coosje L. S. Veldkamp, Hilde E. M. Augusteijn, Marjan Bakker, Robbie C. M. van Aert, and Marcel A. L. M. van Assen. 2016.
“Degrees of Freedom in Planning, Running, Analyzing, and Reporting Psychological Studies: A Checklist to Avoid p-Hacking.” Frontiers in Psychology 7.
https://www.frontiersin.org/articles/10.3389/fpsyg.2016.01832.
Wickham, Hadley, Mara Averick, Jennifer Bryan, Winston Chang, Lucy D’Agostino McGowan, Romain François, Garrett Grolemund, et al. 2019.
“Welcome to the Tidyverse.” Journal of Open Source Software 4 (43): 1686.
https://doi.org/10.21105/joss.01686.
Yarkoni, Tal. 2009.
“Big Correlations in Little Studies: Inflated fMRI Correlations Reflect Low Statistical PowerCommentary on Vul Et Al. (2009).” Perspectives on Psychological Science 4 (3): 294–98.
https://doi.org/10.1111/j.1745-6924.2009.01127.x.